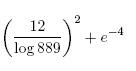1063 - Felicidades

Les deseo a todos un muy Feliz

201x3 + 201x3 + 201x3 + 201+3

Si lo quieres compartir o guardar

1063 - Felicidades

1062 - Cuadrado mágico de 14 x14 con números primos consecutivos

El siguiente es un cuadrado mágico de 14 x 14 que tiene todos los números primos entre el 89 y el 1367

Fue descubierto por Natalia Makarova y lo vi en Prime Puzzles

Si lo quieres compartir o guardar

1062 - Cuadrado mágico de 14 x14 con números primos consecutivos

1061 - Los dos años que vienen

2013 =  3 x 11 x 61   y  2013 + 3 + 11 + 61  =  2088

2014 =  2 x 19 x 53  y   2014 + 2 + 19 + 53 =  2088

Si lo quieres compartir o guardar

1061 - Los dos años que vienen

1060 - 2013 en las potencias de 2

2¹⁸⁹ =  784637716923335095479473677900958302012794430558004314112

¿Cuál es la primer potencia de 2 que tiene "2013" dentro ?

¿y las siguientes?

Si lo quieres compartir o guardar

1060 - 2013 en las potencias de 2

1059 - Del uno al siete

( (1 + 5) x 2 x 4 x 6 x 7) - 3 = 2013

Otras expresiones que den 2013 con los dígitos del 1 al ..n?

Mmonchi mando esta :

2⁽⁵⁺⁶⁾- 34 - 1 = 2013

Rafael Cerezo estas otras :

2 x (4⁵) - 36 + 1 = 2013
7 x (251 + 36) + 4 = 2013  

Si lo quieres compartir o guardar

1059 - Del uno al siete

1058 - Concatenando las potencias de 2013

2013⁰ =  1
2013¹ = 2013 
2013² = 4052169
2013³ = 8157016197 
2013⁴ = 16420073604561
2013⁵ = 33053608165981293
2013⁶ = 66536913238120342809
2013⁷ = 133938806348336250074517 
2013⁸ = 269618817179200871400002721
2013⁹ = 542742678981731354128205477373
2013¹⁰ = 1092541012790225215860077625951849
2013¹¹ = 2199285058746723359526336261041072037
                   

Concatenando obtenemos un número de 225 dígitos

1201340521698157016197164200736045613305360816598129366536913238120342809
1339388063483362500745172696188171792008714000027215427426789817313541282
0547737310925410127902252158600776259518492199285058746723359526336261041
072037



El cual es un número primo 

Si lo quieres compartir o guardar

1058 - Concatenando las potencias de 2013

1057 - 2013 en los tripletes pitagóricos

¿En cuántos tripletes pitagóricos aparece el 2013, teniendo en cuenta los tripletes primitivos y los no primitivos?

¿Hay alguno en el que aparece como hipotenusa?

Si lo quieres compartir o guardar

1057 - 2013 en los tripletes pitagóricos

1056 - 2013 como suma de cuatro cuadrados

¿De cuantas  formas diferentes puede expresarse 2013 como suma de cuatro cuadrados?

Por ejemplo : 0²+ 2²+ 28²+ 35² = 2013

Si lo quieres compartir o guardar

1056 - 2013 como suma de cuatro cuadrados

1055 - 2013 en factoriales

106! = 11462805637347083545343473841483494287038848742413967338
9282723476762012382449946252660360871841673476016298287
0964351437473505282282243025063116800000000000000000000
00000

¿Cuál es el primer factorial que tiene a "2013" dentro?

Si lo quieres compartir o guardar

1055 - 2013 en factoriales

1054 - 2013 en base 13

2013 en base 13 es ..... BBB

Si lo quieres compartir o guardar

1054 - 2013 en base 13

1053 - 2013 como suma de nueve cubos

¿De cuantas maneras se puede expresar 2013 como suma de 9 cubos?

Ejemplo : 

0³+1³+1³+1³+1³+1³+2³+10³+10³ = 2013

Si lo quieres compartir o guardar

1053 - 2013 como suma de nueve cubos

1052 - 2013 como suma de potencias en orden ascendente

El 2013 puede expresarse como suma de potencias en orden ascendente de muchísimas maneras.

2013 = 594¹ + 8² + 3³ + 6⁴ + 2⁵

^{En este ejemplo  no hay dígitos repetidos en las bases y la suma de las mismas es 613.
Existen varias expresiones como esta con 6, 7 y 8 dígitos diferentes en las bases},
 ¿Cuál es la expresión de 2013 como suma de cinco potencias ascendentes, que tiene bases en las que no se repiten dígitos y la suma de las mismas es la menor posible (para 6, 7 y 8 dígitos)? ¿y la expresión con la mayor suma de las bases?

Si lo quieres compartir o guardar

1052 - 2013 como suma de potencias en orden ascendente

1051 - La tabla de primos del 2013

Siguiendo con los artículos relacionados con el año que viene, les presento la siguiente tabla  compuesta exclusivamente por números primos :

Elijan un primo cualquiera hagan un círculo alrededor de él, y tachen los primos restantes que forman parte de la misma columna y los que forman parte de la misma fila que el primo elegido. Les quedara entonces un número marcado y ocho tachados, elijan ahora cualquier otro primo de los no tachados y repitan la misma operación, continúen haciendo esto hasta que queden solo cinco números marcados y todos los demás tachados.

Sumen los números marcados y .... ♫ tatan ♫ tatan  ♪ .... la suma les debe dar 2013.


¿Porqué funciona?

Les explico el truco, si vamos a usar una tabla de cinco por cinco, necesitamos diez números llamados iniciales cuya suma sea igual al valor que queremos, en este caso, 2013. Una vez que tenemos estos diez números, colocamos cinco encima de la tabla que vamos a graficar y los otros cinco a la izquierda de la tabla en forma vertical.
Los números que yo elegí son el 5, 6, 54, 95, 103, 125, 168, 185, 306 y 966.
Coloqué los impares sobre la tabla y los pares a la izquierda de la misma :

Lo que hay que hacer ahora es completar la tabla colocando en cada casilla la suma de los números iniciales relacionados con dicha casilla (el que está arriba, en la misma columna, y el que está a la izquierda en la misma fila), como se ve en el siguiente dibujo :

Ahora borramos las números iniciales y listo.
La suma siempre da 2013 porque cuando elegimos un número estamos eligiendo la suma de los dos números que le dieron origen, y al borrar los de la columna y los de la fila nos aseguramos que estos números no se vuelvan a sumar, al finalizar el proceso quedaran cinco números cuya suma es igual a la suma de los 10 números iniciales o sea en este caso, 2013. Yo hice una variante de forma tal que la suma de cada dos números iniciales sea siempre un número primo.

Si lo quieres compartir o guardar

1051 - La tabla de primos del 2013

1050 b -2013 elevado a... II

Dentro de 2013⁶⁰ aparece el 2011:

17006952287782399043161889746164190186653170491256218703 10084828015758080339135822270322960509264254918942798932 73900364221528277816426444053481650422011783213485423365 2830730398244513006526731876401 Pero lamentablemente no aparece el 2013. ¿Aparecerá dentro de alguna potencia (distinta de 1) el 2013?

Si lo quieres compartir o guardar

1050 b -2013 elevado a... II

1050 - 2013 elevado a ... I

En 2013⁶ aparece el seis en la primera, en la segunda y en la quinta  posición:
 2013⁶ = 66536913238120342809

En 2013⁴ aparece el cuatro en la tercera y en la undécima posición
 2013⁴ = 16420073604561

En 2013⁵ aparece el cinco en la cuarta y en la undécima posición
 2013⁵ = 33053608165981293

a) No encontré una potencia n tal que 2013ⁿ de como resultado un número, en el cual n aparezca en la quinta posición ¿Habrá alguno?

En 2013⁵⁸ aparece el 58 en las posiciones 26, 32, 55, 59 y 79.
 Vemos que por muy poquito el 58 no aparece en la posición 58.
2013⁵⁸ = 419699975193097796344670958841158653221353070201569053588358439150923389507973587051853701192932539318805015025962392891859960129541552793216377822400822332961644549783790046860889689696191529

b)¿Habrá algún número n, tal que 2013ⁿ sea un número en el cual n aparezca en la posición n?

Si lo quieres compartir o guardar

1050 - 2013 elevado a ... I

1049 - Demostración del teorema de pitágoras con .... agua

Si lo quieres compartir o guardar

1049 - Demostración del teorema de pitágoras con .... agua

1048 - 2013 como suma de tres primos

2013 puede expresarse como suma de tres primos de varias maneras, pero hay cinco que usan los mismos dígitos (dos 1´s, dos 3´s, un 7 y dos 9´s)
 
3+79+1931 = 3+97+1913 = 3+13+1997 = 3+17+1993 = 3+31+1979 = 2013


¿Habrá otra/s combinaciones que entre ellas usan los mismos dígitos entre las 2253 formas de expresar 2013 como suma de primos?

Si lo quieres compartir o guardar

1048 - 2013 como suma de tres primos

1047 - Sumando 2013

Se acerca el 2013, es por ello que a partir de hoy y hasta el 21 de diciembre, pondré varios problemas curiosidades y expresiones relacionados con dicho número.
Aquí va el primero:

Los divisores propios de 4323 son : 1, 11, 33, 131, 393 y 1441.
Si los sumamos  obtenemos 1+11+33+131+393+1441 = 2013

¿Cuantos números hay como el 4323, tal que la suma de sus divisores propios da 2013?

Si lo quieres compartir o guardar

1047 - Sumando 2013

1046 - El mayor primo que

¿Cuál es el mayor primo tal que la diferencia de cualquiera dos dígitos de él da un número primo?

Por ejemplo el 257 es uno de estos números ya que 5-2 , 7-2 y 7-5 son todos números primos

Si lo quieres compartir o guardar

1046 - El mayor primo que

1045 - Tirando monedas

Alfredo, Bernardo y Casimiro tiran al aire una moneda 15, 16 y 17 veces respectivamente.
Al día siguiente tiran 15, 17 y 20 respectivamente
El tercer día las tiran 18, 19 y 20 veces

¿Quién tiene menos posibilidades de sacar mas caras que secas, cada día?

Si lo quieres compartir o guardar

1045 - Tirando monedas

1044 - Dividiendo multiplicando y sumando

Existe una sola forma de dividir los números uno y dos en dos grupos :
1 - 2  el producto es 2 (1x2) y la suma de los productos también , que en este caso es uno solo, también es 2

Los números del 1 al 4 en cambio se pueden dividir de varias maneras en dos grupos.
Algunos ejemplos:

(12) (34) suma de los productos 1x3 + 2x4 = 3 + 8 = 11  
(12) (43) suma de los productos 1x4 + 2x3 = 4 + 6 = 10
(13) (24) suma de los productos  1x2 + 3x4 = 2 +12 = 14
(23) (41) suma de los productos  2x4 + 3x1 = 8 + 3 = 11

Luego de buscar todas las combinaciones posibles, la suma máxima de los productos es 14

Para los números del 1 al 6 la siguiente división en dos grupos da la mayor suma de los productos::
(136) (245) suma de los productos  1x2 + 3x4 + 6x5 = 2 + 12 + 30 = 44


¿Cuál es la mayor suma de los productos de la división en dos grupos de los números del 1 al 8? y del 1 al 10? ¿Alguien puede deducir la fórmula?

Si lo quieres compartir o guardar

1044 - Dividiendo multiplicando y sumando

1043 - Menor primo

¿Cuál es el menor primo que no divide a ninguno de los números que están entre 2000 y 2100?

¿y entre 20000 y 21000?

Si lo quieres compartir o guardar

1043 - Menor primo

1042 - Nació usted en una fecha interesante?

¿Cómo saber si naciste en una fecha interesante?
Fácil,  multiplica el día  x N° mes x año.
Ahora divide el resultado por 77, el número obtenido dividelo por 13.
Si obtienes un número sin decimales tu fecha de nacimiento es interesante

Si en cambio obtienes un número con decimales suma los primeros seis.

Listo?

Si la suma te dio 27 sos un ser excepcional!

Esta entrada participa en la Edición 3.14159265 del Carnaval de Matemáticas cuyo anfitrión es el blog PiMedios: La aventura de las matemáticas.

Si lo quieres compartir o guardar

1042 - Nació usted en una fecha interesante?

1041 - Múltiplo de 11

¿Qué número de tres cifras no es múltiplo de 11 y no puede transformarse en uno aunque le cambiemos solo uno de sus dígitos?

Si lo quieres compartir o guardar

1041 - Múltiplo de 11

1040 - Sin palabras

1) Pi

La animación es de John Reid


2) Teorema de Pitágoras

 Animación de Joaquim Alves Gaspar

3) Como hacer una hipotrocoide

Animación de Sam Derbyshire

4) Hipercubo

Animación de Jason Hise

  


Los gifs los obtuve de 20 gif que explican como funcionan las cosas
  
Esta entrada participa en la Edición 3.14159265 del Carnaval de Matemáticas cuyo anfitrión es el blog PiMedios: La aventura de las matemáticas.

Si lo quieres compartir o guardar

1040 - Sin palabras

1039 - Todos los dígitos en dos potencias

18³ = 5832
18⁴ = 104976
y
69² = 4761
69³ = 328509

Vemos que un mismo número elevado a dos potencias origina dos números que entre los dos tienen todos los dígitos una sola vez

La idea es encontrar números que elevados a dos potencias distintas den números que tengan exactamente n veces todos los dígitos. Donde n = 2, 3, 4, etc

Obviamente que los casos triviales en donde elvamos a la cero y a la primera no los consideramos
(ejemplo 12233445566778899⁰ y 12233445566778899¹)

Si lo quieres compartir o guardar

1039 - Todos los dígitos en dos potencias

1038 - Buscando primos en pi II

En esta ocasión busqué primos en pi al revés (como en la entrada 1035), pero sin considerar el 3 inicial.
Así encontré : 41, 6295141, 5356295141, ...

¿Cuál es el mayor primo que pueden encontrar de está forma?


Pd : en este enlace están los primros 100000 dígitos de pi

Si lo quieres compartir o guardar

1038 - Buscando primos en pi II

1037 - Pagando 2010 con billetes de 2, 5 y 10

Matías quiere comprarse una tablet que cuesta $2010. 
Sus ahorros los tiene en billetes de $2, de $5 y de $10. 
Cuando contó la plata se dio cuenta de que con los billetes que tenía podía pagar los $2010, todo con billetes de dos, o todo con los de cinco o todo con los de diez u obviamnente con  una combinación de estos.

¿De cuántas formas diferentes puede pagar Matías los $2010?


Adapatado de un problema del Mit.

Si lo quieres compartir o guardar

1037 - Pagando 2010 con billetes de 2, 5 y 10

1036 - El número secreto

De estas diez sentencias sobre un número secreto,  5 son verdaderas y 5 son falsas
En cada par de sentencias con el mismo número una es verdadera y otra falsa.
Descubra cual es cual y determine cual es el número secreto

1a. Tengo dos dígitos
1b. Soy par

2a. Tengo un siete
2b. Soy primo

3a. Soy el producto de dos números impares consecutivos
3b. Soy un número mas grande que un cuadrado perfecto

4a. Soy múltiplo de 11
4b. Soy un número mas grande que un cubo perfecto

5a. Soy un cuadrado perfecto
5b. Tengo tres dígitos

¿Qué número soy?

Visto en Internet

Si lo quieres compartir o guardar

1036 - El número secreto

1035 - Buscando primos en pi

 Pi = 3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006.....
 

Es bien conocido que dentro de de pi hay de todo lo que uno quiera buscar y también números primos....
Así, que alguien se dedicó a buscar primos en la expansión decimal de pi y se encontraron entre otros los siguientes primos : 3, 31, 314159, 31415926535897932384626433832795028841, etc . 
Se puede ver la serie completa en la OEIS

Yo me dediqué a buscar primos en pi pero de una forma distinta, (y si, soy medio complicado)
En vez del derecho, los busqué del revés (es decir desde los decimales hasta el 3), así encontré : 3, 13 , 51413, 951413, 2951413, 53562951413, etc...

¿Cuál es primo mas largo que pueden encontrar de esta forma?


Pd : en este enlace están los primeros 100000 dígitos de pi

Si lo quieres compartir o guardar

1035 - Buscando primos en pi

1034 -Como acordarse del valor de raíz cuadrada de 2 y de la raíz cuadrada de 0.5

El otro día leí en el excelente blog ZTFNews un artículo que explicaba como acordarse el valor de e.
Hace un tiempo me habían enseñado a acordarme del valor de Raíz cuadrada de 2.
Para ello solo hay que recordar esta secuencia : 2, 2, 3, 5 y 9  fácil no?
¿Y como se relaciona esto con la raíz cuadrada de 2?

Solo debemos multiplicar cada término por 7 :
14 14 21 35 63
Ponemos la coma y obtenemos una buena aproximación a la raíz cuadrada de 2
1.414213563, el verdadero valor es 1.41421356237....

Para calcular la raíz cuadrada de 0.5 dividimos por dos cada término anterior =

1.4 / 2     = 0.7                     
0.014 / 2 = 0.007                 
 0.00021 / 2  = 0.000105           
  0.0000035 / 2 = 0.00000175       
0.000000063 / 2  = 0.0000000315   
------------------- +

Raíz cuadrada de 0.5  = 0.7071067815    

Lo cual  es correcto salvo el último decimal

Si lo quieres compartir o guardar

1034 -Como acordarse del valor de raíz cuadrada de 2 y de la raíz cuadrada de 0.5

1033 -Completar con los números del 0 al 9

Reemplazar los signos de preguntas por dígitos, al finalizar deben estar presentes todos los números del 0 al 9, y además, ya que estamos,  la cuenta debe ser correcta. 
Como ayuda (?) les pongo el 1

     ???
  x   ??
 --------
  ????1

Del libro Puzzles in math and logic de A Friedlan

Si lo quieres compartir o guardar

1033 -Completar con los números del 0 al 9

1032 - Sin usar calculadora y/o computadora y/o...

2²⁹ tiene todas los dígitos menos uno, sin hacer la cuenta,  
¿Sabrían decirme cual es el dígito que falta?
 


Justificar (como en el colegio, jaja)

Si lo quieres compartir o guardar

1032 - Sin usar calculadora y/o computadora y/o...

1031- Sumando edades

- Sabes que mis tres primos lejanos y yo tenemos todos edades primas, y que la suma de nuestras edades es 50 ?.
- Ah, entonces te puedo decir las edades de tus primos rapidamente
- Que vivo, vos por que sabes mi edad

y usted ¿Podrá ?



Adaptado del libro Puzzles in math and logic de A Friedlan

Si lo quieres compartir o guardar

1031- Sumando edades

1030 - Jugando con los factoriales

El 1 es el menor número que aparece en la primer posición de su propio factorial.
El 4 es el menor número aparece en la segunda posición de su propio factorial 4! = 24
El 39 es el menor número que aparece en la tercer posición de su propio factorial :
  39! = 20397882081197443358640281739902897356800000000
El 33 es el menor número que aparece en la cuarta posición de su propio factorial :
  33! = 8683317618811886495518194401280000000
El 37 es el menor número que aparece en la quinta posición de su propio factorial :
  37! = 13763753091226345046315979581580902400000000

Hay que notar que tanto el 39 como el 37 aparecen dos veces en su propio factorial.

En el factorial de 80, el 80 aparece cuatro veces :
71569457046263802294811533723186532165584657342365752577109445058227039255480148842668944867280814080000000000000000000

a)¿Cuál es el menor número que aparece en la posición 6 de su factorial?
b)¿Cuál es el menor número que aparece exactamente tres veces en su factorial?
c)¿Existirá algún factorial de un número N (además del uno), tal que dicho número N aparece  en la posición N?

Si lo quieres compartir o guardar

1030 - Jugando con los factoriales

1029 - Acorralando a Pi

Muchos sabemos que pi es aproximadamente 22/7 (3.1428..)
, este valor ya era conocido por Arquímedes, posteriormente se hicieron mayores aproximaciones como 355/113  (3.141592920...)
que es correcto hasta el sexto decimal.
 
 Pero existen otras expresiones que se acercan mas a pi:

Esta fórmula tiene una precisión cercana a 2 x 10^-14
En tanto que la siguiente:

da pi con 15 decimales correctos como vemos en :

Si les asombra esta expresión , calculen :

Tiene con 1/pi una diferencia de solo 2 x 10^-19




Fuentes : wikipedia y este pdf de William H. Press

Si lo quieres compartir o guardar

1029 - Acorralando a Pi

1028 - Dividiendo los digitos

- El otro día estuve jugando con mi sobrino
- Al fútbol?
- Un rato, pero antes jugamos con los números
- Que tío divertido...
- Lo que pasa es que está un poco flojo en matemáticas y aproveché para que practicara la multiplicación
- ¿Cómo era el juego?
- Elegíamos por turnos, uno de los 9 dígitos, hasta que uno tuviera 5 y el otro 4. El que tenía cinco formaba dos números y los multiplicaba, el otro debía formar también dos números de forma tal que su producto se aproximara lo mas posible al resultado del primero. Hay que tener en cuenta que cada dígito se usaba una sola vez.
- ¿Y la anécdota?
- En una de la vueltas a mi sobrino le tocaron los 5 dígitos y formó un producto que tenía dos ceros, y yo con los otros cuatro dígitos pude formar dos números que multiplicados daban el mismo resultado.
- Guau, y eso es raro?
- Parece que no mucho porque en la vuelta siguiente pasó lo mismo pero el producto que obtuvimos era otro.

Si lo quieres compartir o guardar

1028 - Dividiendo los digitos

1027 - Con cien dígitos

Supongamos que elegimos 100 digitos al azar, 
¿Cuál es la probabilidad de que con ellos podamos formar dos números a y b, tal que a^2 = b ?
Los cien dígitos deben formar parte de a o de b.
Obviamente que no son válidos los números que empiezan con cero

Un ejemplo : con tres dígitos en vez de cien, a y b podrían ser respectivamente : 4,16 - 5, 25 - 6, 36 - 7, 49 - 8, 64 - o 9 ,81 . Pero con 357, 117, o 669 no se podría formar ningún par a,b.


Del libro Puzzles in math and logic de A. Friedlan

Si lo quieres compartir o guardar

1027 - Con cien dígitos

1026 - Otros como el 15251

En Prime Curios! aparece el número 15251 como el menor número capicúa tal que la suma de los números primos que van desde el menor factor hasta el mayor factor es un número primo, como así también la suma de los compuestos entre estos dos factores.
Haciendo los cálculos : 
15251 = 101 x 151
y 
101 + 103 + 107 + 109 + 113 + 127 + 131 + 137 + 139 + 149 + 151 = 1367 (primo)
102 + 104 + 105 + 106 + 108 + 110 +  …  + 146 + 147 + 148 + 150 = 5059 (primo)


Leyendo el título de la entrada se imaginarán cual es la pregunta del día.
¿Cuales son los que siguen?
¿Cuál es el mas grande que pueden encontrar?

Si lo quieres compartir o guardar

1026 - Otros como el 15251

1025 - Dividiendo 1025

- Así que llegaste a las 1025 entradas?
- Estoy en eso  - contesté
- Te propongo un problema entonces
- Te escucho
- Suponé que divido 1025 figuritas en dos pilas, del tamaño que vos quieras
- Ahá
- Ahora contá cuantas figuritas tenes en cada pila y multiplicá los números obtenidos
- Fácil, yo había pensado una figurita por un lado y 1024 por el otro, así que el producto es 1024
- Ok, ahora, yo divido la pila que tiene mas de una figurita y hago lo mismo. Por ejemplo divido las 1024 en una pila de 1000 y  otra de 24, el producto me da 24000. A este valor lo sumo al resultado anterior 24000+1024 = 25024.  
Lo que tenes que hacer ahora es dividir cada una de las pilas que quedaron, en dos, calcular los productos y sumarlos al resultado anterior
- Y después?
- Seguimos dividiendo,  multiplicando y sumando hasta que queden 1024 pilas de una figurita.
- Ahá, y ?
- La pregunta es ¿Cuanto va a dar la suma total?

Si lo quieres compartir o guardar

1025 - Dividiendo 1025

1024 - Números que se transforman

En los siguientes números si concatenamos los largos de las palabras que forman al mismo número obtenemos una permutación del número original.
Curiosamente, o no, los ejemplos que encontré usan solo dos grupos de números: 

13570   = Trece mil quinientos setenta
 Letras =     (5)    (3)     (10)         (7)        =  53107

 70513 = Setenta mil quinientos trece
 Letras =     (7)     (3)       (10)       (5)      =  73105



13615  = Trece mil seiscientos quince 
Letras  =  (5)    (3)        (11)         (6)       =  53116
 
15613  = Quince mil seiscientos trece 
Letras  =     (6)    (3)       (11)         (5)     =  63115



 Habrá ejemplos con números  de mas cifras?

   

Si lo quieres compartir o guardar

1024 - Números que se transforman

1023 - Dados quien empieza

Imagínese que usted desea jugar un juego con 2-4 jugadores, y es necesario determinar aleatoriamente quién juega primero. Si cada uno de ustedes simplemente tirara un dado estándar, hay una buena probabilidad de que haya empates, ustedes tendrían que volver a tirar los dados y nadie quiere eso.
Estos dados diseñados por Eric Harshbarger resuelven este problema:

Son dados de doce caras cada uno, los cuales entre los cuatro, tienen escritos los números del 1 al 48 y fueron diseñados para que cumplan las siguientes condiciones:

a - Nunca habrá un empate
b - Independientemente de que grupo de dados sean tirados, todos los jugadores tienen la misma chance de obtener el número mas alto y por lo tanto de ser el ganador. Dicho de otro modo, dos, tres, o cuatro jugadores pueden tomar cada uno de los dados, tirarlos, y cada uno tendrá siempre una probabilidad de 1/2, 1/3 o 1/4, respectivamente, de obtener el resultado más alto.
c - Finalmente, no sólo pueden usarse todos los dados (o cualquier subconjunto) para determinar el primer jugador, sino que los números obtenidos también se pueden usar para determinar todas las posiciones de partida (el segundo número más alto puede ser el segundo jugador, el tercero más alto el tercer jugador, etc) ya que la probabilidad de cada una de las permutaciones de cualquier subconjunto determinado de dados es la misma, por lo que nunca habrá la posibilidad de que un subconjunto particular favoreciera a algunos de los jugadores.

Aquí están los números de cada uno de los dados:

D1: 1, 8, 11, 14, 19, 22, 27, 30, 35, 38, 41, 48
D2: 2, 7, 10, 15, 18, 23, 26, 31, 34, 39, 42, 47
D3: 3, 6, 12, 13, 17, 24, 25, 32, 36, 37, 43, 46
D4: 4, 5, 9, 16, 20, 21, 28, 29, 33, 40, 44, 45


Si arrojamos dos dados cualesquiera, por ejemplo el 1 y el 3 , tenemos 144 resultados posibles, y en la mitad ellos gana el dado 1 en tanto que en la otra mitad gana el 3.

Si arrojamos tres de los dados, por ejemplo el D1, D2 y el D3, tenemos 12³ = 1728 resultados posibles y el orden de los dados será  [D1,D2,D3] en 288 ocasiones, lo mismo para cualquiera de las otras cinco permutaciones [D1,D3,D2], [D2,D1,D3], [D2,D3,D1], [D3,D1,D2] y [D3,D2,D1

En tanto que al tirar los cuatro dados, hay 20736 resultados posibles, y cada dado ganará en  5184 ocasiones, y cada una de las 24 permutaciones [Da,Db,Dc,Dd] se da exactamente en 864 de las 20736.

Se puede ver todas las combinaciones y sus probabilidades aquí.


Esta entrada participa de la Edición 3,1415926 del Carnaval de Matemáticas, cuyo anfitrión es el blog Series Divergentes.

Si lo quieres compartir o guardar

1023 - Dados quien empieza

1022- Números de nueve digitos

¿Cuántos números de nueve dígitos hay, tal que no tengan tres dígitos repetidos y consecutivos?

Ejemplos de estos números serían 112234588, 552781234, 121212121 en tanto que 123444567 no cumple la condición (tiene tres dígitos repetidos y consecutivos : 444)

Si lo quieres compartir o guardar

1022- Números de nueve digitos

1021 - Primos cercanos a potencias de 10

El siguiente número que tiene 239 cifras es primo :

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999989

Este otro tiene 203 cifras

1000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000009

Si lo quieres compartir o guardar

1021 - Primos cercanos a potencias de 10

1020 - Seiscientos once nonillones setecientos dieciseis

Tratando de resolver  el problema 658 planteado en PrimePuzzles, encontré unos números curiosos que serían la versión española del número encontrado por Eric Harshbarger.
Es muy fácil encontrar números que tienen en su composición una cantidad  diferente de cada dígito, por ejemplo 122333, tiene un 1, dos 2 y tres 3,  podemos encontrar  infinitos de estos números. Inclusive podemos escribir números que tengan un digito una vez, otro dos, el tercero, tres, así hasta nueve o diez. Pero con las letras de los nombres de los números no ocurre lo mismo.

Seiscientos once nonillones setecientos dieciseis es un número que tiene 57 dígitos (un 7, dos 6, tres 1 y cincuenta y un 0), pero además tiene exactamente : 
1 d, 2 l, 3 t, 4 c, 5 o, 6 n, 7 i, 8 s y 9 e.

En tanto que :
Un octodecillón doscientos cinco nonillones seiscientos cinco tiene 109 dígitos pero además tiene exactamente: 
1 u, 2 d, 3 t, 4 l, 5 e, 6 s, 7 i, 8 c, 9 n y 10 o.
y
Doscientos doce millones doscientos dieciséis mil setecientos veinticinco tiene 1 v, 2 m, 3 l, 4 d, 5 t, 6 n, 7 c, 8 e, 9 s, 10 e y 11 i.

 ¿Serán estos los menores números en español con este tipo de característica?

Carlos Rivera me comenta que él encontró :
Mil trescientos veintiseis millones seiscientos cinco mil novecientos once que es el menor número primo con las siguientes características:
r=1, v=2, m=3, l=4, t=5, c=6, o=7, n=8, s=9, e=10, i=11

Si lo quieres compartir o guardar

1020 - Seiscientos once nonillones setecientos dieciseis

1019 - Tirando monedas

Juguemos  un juego con monedas.
 
Tu tienes 100 monedas de diez centavos, y yo tengo 99 monedas de cinco centavos. 
Al mismo tiempo, echamos nuestras monedas al aire y las dejamos caer en el suelo. 
Luego contamos meticulosamente los resultados de nuestros lanzamientos.

Tu ganas si logras más caras que las que yo obtengo. 

¿Cuál es tu probabilidad de ganar?



Un problema  de Presh Talwalkar

Si lo quieres compartir o guardar

1019 - Tirando monedas

1018 - Múltiplos con menor suma de sus dígitos

Simple :
¿Cuál es el menor múltiplo de 29 cuya suma de sus dígitos es la menor posible?
Por ejemplo 58 (29x2) tiene suma 13, pero 116 (29x4)  tiene suma 8 y 203 (29x7) tiene suma 5

Complicado :
¿Cuál es el menor múltiplo de 97 cuya suma de sus dígitos es la menor posible?


Difícil:
¿Cuál es el menor múltiplo de 313 cuya suma de sus dígitos es la menor posible?

Si lo quieres compartir o guardar

1018 - Múltiplos con menor suma de sus dígitos

1017 - Pintando con Camila

A Camila le regalaron seis potes de pintura, uno rojo, uno azul, uno amarillo, uno verde, uno celeste y uno rosa.
Todos los días ella píntaba un cuadro. Los cuadros de Camila consistían en rectángulos del mismo tamaño, uno al lado del otro pero de distintos colores
Habiá días en que usaba cada color por separado, por ejemplo hacía primero una rectángulo rojo, después uno azul, una amarillo, uno verde, uno celeste y por último uno rosa

 Una vez que había pintado en un determinado orden, no lo volvía a repetir. Así que estuvo pintando varios días hasta que no pudo pintar un nuevo cuadro sin que fuera igual a alguno que ya había pintado.
Fue ahí que empezó a mezclar colores, así un día mezcló el rojo con el azul y pintó el primer rectángulo con ese color y los otros con los otros colores, claro que los dias siguientes pudo seguir usando esta combinación hasta que no puedo seguir pintando sin repetir alguno de los cuadros ya pintados. Mezcló entonces otros dos colores y siguió pintando.  Cuando se le acabaron los cuadros, mezcló tres, después cuatro y hasta cinco colores, una vez que terminó todas las combinaciones posibles, pintó un último cuadro que consistía en un solo rectángulo con todos los colores mezclados.


¿Cuántos cuadros pintó Camila?

Si lo quieres compartir o guardar

1017 - Pintando con Camila

1016 - Acceso libre al archivo de revistas matemáticas

En el sitio Elsevier colocaron los links al archivo de varias revistas matematicas:

Si lo quieres compartir o guardar

1016 - Acceso libre al archivo de revistas matemáticas