Las reglas de divisibilidad son criterios que sirven para saber si un número
es divisible por otro sin necesidad de realizar la división.
Para los primeros números primos existen reglas muy simples que todo el mundo conoce, que aquí las repito:
Un número es divisible por 2 si termina en un número par
Un número es divisible por 3 si la suma de los dígitos de dicho número es múltiplo de 3
Un número es divisible por 5 si termina en cero o cinco
Pero que pasa para números primos mas grandes?
Existe un método que permite generar una regla para cada número primo. En esta entrada les voy a explicar como saber si un número es divisible por un número primo determinado sin tener que hacer la división, porque el método funciona y como obtener los números que permiten hacer estos cálculos.
El método se basa en una acción recursiva sobre el número original, haciéndolo cada vez mas pequeño hasta lograr un número que nos permita saber si es múltiplo o no del primo elegido.
Cada número primo tendrá dos números asociados (uno positivo y otro negativo) que permitirán ir disminuyendo el valor del número original hasta que tome un valor tal del cual podamos decir si es o no múltiplo del primo elegido
Voy a explicarlo usando un ejemplo:
Es 28373 divisible por 17?
Los números asociados al 17 son -5 y 12
Lo que hay que hacer es dividir el número en dos partes en la primera entran todos las cifras menos la última, que es la que se multiplica por el número asociado y el resultado se suma a la primera parte. Así 28373 lo divido en 2837 y 3, y al 3 lo multiplico por el número asociado y lo sumo:
28373 :
2837 + (
3 x -5) = 2837-15 = 2822
como no sabemos si 2822 es múltiplo de 17 repetimos el proceso :
2822 :
282 + (
2 x -5) = 282 -10 = 272
una vez mas :
272 :
27 + (
2 x -5) = 17
Por lo tanto 28373 es múltiplo de 17 (obviamente que también lo son 2822 y 272)
Usando el 12 en vez de -5 :
28373 : 2837 + 3 x 12 =2873
2873 : 287 + 3 x 12 =323
323 : 32 + 3 x 12 = 68
y como 68 es múltiplo de 17, 28373 también lo es.
Como encontrar los números asociados?
Hay buscar el menor múltiplo del primo que termine en 1, así por ejemplo para el 17 este número es el 51 (3 x 17).
Uno vez obtenido este múltiplo, el número asociado son todos los dígitos de este número sin el último, multiplicado por -1. Así obtenemos el -5, el otro número asociado
sale de la suma del primo mas este primer número, o sea 17 - 5 = 12
Otro ejemplo , si el primo es 19 el menor múltiplo terminado en 1 es 19 x 9 = 171, entonces los número asociados son -17 y 2.
Si el primo termina en uno, el número asociado es el negativo de los primeros dígitos del primo.
Así para el 31 , -3 es uno de los números (28 es el otro)
Porque funciona?
Veamoslo con el 17
Si el número N es múltiplo de 17 entonces
N = 17a = 10 P + U
donde P = primeros dígitos de N, salvo el último y U = último dígito de N
Si multiplicamos por -5 ambos miembros :
17 (-5a) = -50P - 5 U
Sumando 51P a ambos miembros (noten que 51 es el menor múltiplo de 17 terminado en 1) :
17(-5a) + 51P = P -5U
Vemos que en lado derecho tenemos el número que obtenemos después de realizar el primer paso, ahora hay que demostrar que el lado izquierdo es múltiplo de 17
17(-5a) + 17.3.P = 17 (-5a+3P)
Así queda demostrado que si 10P + U es múltiplo de 17, P-5U también lo es.
Tabla de números asociados para los primos hasta el 971
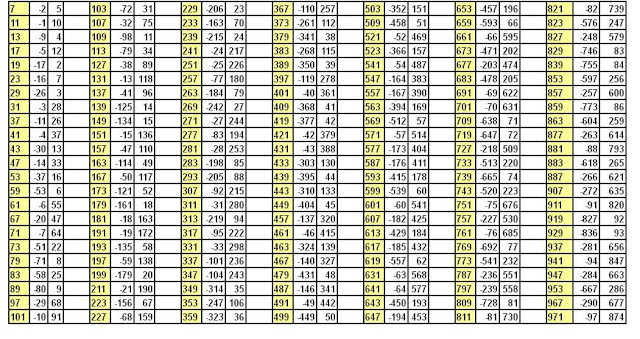 |
| Hacer Click sobre la imágen para ver el cuadromas grande |
Analizando un poco la tabla podemos calcular mas rápido los números asociados :
Si el test es para un
primo terminado en 9 (xxxxx9), y el número a evaluar es M,
el número asociado positivo es uno mas que los primeros dígitos del primo
Ej para saber si un número M es divisible por el primo 269, se multiplica el último dígito de M por 27 y se suma a lo que queda.
M= 2152 : 215 2
Primo = 269, número asociado uno mas que los primeros dígitos = 27
2152 : 215 + 27*2 = 269 , por lo tanto 2152 es múltiplo de 269
Si el test es para un número
primo terminado en 1 (xxxxx1), y el número asociado negativo son los primeros dígitos del primo
Ej para saber si un número M es múltiplo del primo 61, se multiplica el ultimo dígito de M por -6 y se suma a los primeros dígitos de M
1037 : 103 - 7*6 = 61, por lo tanto 1067 es múltiplo de 61
El numero asociado positivo en
primos terminados en 7 es 7 x primeros números del primo mas 5,
ej para el primo 13687: 7 x 1368 +5 = 9581
El numero asociado positivo para
primos terminados en 3 es 3 x primeros números del primo + 1
ej para el primo10273: 3 x 1027 + 1 = 3082
Esta entrada forma parte del
carnaval de matemáticas que en esta ocasión organiza
tito eliatron
Si lo quieres compartir o guardar

1084 - Criterios de divisibilidad


 y así obtenemos la fracción que en base 36 es 0.numerosnumeros....
y así obtenemos la fracción que en base 36 es 0.numerosnumeros....