Un golígono (técnicamente llamado "isógono serial de 90 grados") es cualquier polígono con todos los ángulos rectos, cuya longitud de los lados son una secuencia de números enteros. Los golígonos fueron inventados y nombrados por Lee Sallows, y popularizados por A.K. Dewdney en la columna de Scientific American de 1990.
Así lo presentaban en la revista:
"Permítanme introducirlos a un viaje en Golygon City. Usted puede realizar un viaje similar en Nueva York, Kioto o en casi cualquier gran ciudad cuyas calles forman una cuadrícula . Aquí están sus instrucciones. Camine una sola calle de la ciudad en cualquier dirección, al final de la misma gire a la izquierda o a la derecha y. camine dos cuadras más, luego gire nuevamente a la izquierda o a la derecha, y camine ahora otras tres calles mas, y así sucesivamente. Cada vez que gira, debe caminar en línea recta una cuadra más que antes. Si después de una serie de giros llega a su punto de partida, es que ha trazado un golígono. Si usted no quiere hacer ejercicio físico, puede simular fácilmente el viaje al mover un lápiz a lo largo de un pedazo de papel cuadriculado . Si queda perdido, puede ver al mapa a continuación. "
Una forma de describir a un goligono es usando puntos cardinales, así el golígono de la imagen puede describirse como : 1N 2E 3S 4W 5S 6W 7N 8E
Donde N,S, E y W significan Norte, Sur, Este y Oeste
En cualquier golígono, todos los lados horizontales tienen la misma paridad, así como también pasa en los lados verticales. Por lo tanto, el número n de lados debe permitir la solución en un sistema de ecuaciones.
No se permite pasar dos veces por un mismo punto
Un dato interesante es que se puede teselar una superficie usando golígonos:
A partir de allí muchas preguntas surgieron:
a) ¿Cuantos golígonos diferentes de 16 lados existen?
b) ¿Es posible formar golígonos con lados primos?
c) ¿Es posible formar un golígono de 8 lados que empiece en cualquier número diferente a 1?
Todas estas preguntas ya fueron respondidas
a) Es posible formar 72 golígonos distintos de 16 lados
Un ejemplo:
1N 2E 3N 4E 5S 6E 7S 8E 9S 10W 11S 12W 13N 14W 15N 16E
El número total de golígonos de 16 lados es 112.
En la Oeis aparece la siguiente secuencia A007618: 4, 112, 8432, 909288, 121106960, 18167084064, 2956370702688, 510696155882492, 92343039606440064, 17311893232788414400, 3342127071364266721200 que indica la cantidad de golígonos de largo 8n
b) Golígono con 16 lados primos :
1N 3E 5N 7W 11N 13W 17N 19E 23N 29W 31N 37E 41S 43E 47S 53W y
1N 3E 5S 7W 11S 13W 17N 19E 23N 29W 31S 37E 41S 43E 47N 53W
 |
| Golígono con lados primos |
c) ¿Es posible formar un golígono de 8 lados que empiece en cualquier número diferente a 1?
La respuesta es sí :
1N 2E 3S 4W 5S 6W 7N 8E
2N 3E 4S 5W 6S 7W 8N 9E
3N 4E 5S 6W 7S 8W 9N 10E
etc
Podemos seguir indefinidamente porque si vemos las direcciones del primer golígono obtenemos las siguientes ecuaciones
1-3-5+7 =0 y 2-4-6+8 = 0, en los siguientes golígonos lo único que hacemos es sumarle 1 a cada término por lo que la igualdad se mantiene (sumamos y restamos 2)
Lo que preguntó Joe O’Rourke en Mathoverflow era si existia un goliedro, es decir una versión 3D de un golígono.
Adam P Goucher leyó el post y construyó el primer goliedro que se conoce que tiene 32 caras
Adam escribió un post en su blog en el cual explica como lo obtuvo.
Alexey Nigin recientemente descubrió este goliedro mas pequeño de solo 15 lados:
Actualización : Alexey Nigin encontró este Goliedro de 12 lados
Una idea que se me ocurrió leyendo sobre los golígonos es si podía haber alguno en que los lados horizontales fueran números consecutivos desde el 1 hasta n y los verticales los números que van de n+1 hasta 2n.
Evidentemente existen estas figuras ya que por ejemplo 1-2-3+4 = 0 y 5-6-7+8=0
Así por ejemplo podemos formar la siguiente figura 1E 5S 2W 6N 3W 7N 4E 8S
También se pueden hacer polígonos con lados que sean números de Fibonacci con una cantidad de lados horizontales y verticales múltiplos de 3 (ya que siempre Fi + Fi+1 = Fi+2)
Ejemplo: 1E 5S 2E 8S 3W 13N
¿Qué otras variantes para los golígonos se les ocurre?
Pd: aquí está el golígono de 8 lados primos consecutivos que me envió Carlos Rivera, empieza en el 359
y este es el de 16 lados primos consecutivos, también encontrado por Carlos Rivera
Fuentes :
Golígono en Wikipedia
Mathoverflow
Cp4 Golygons and Golyhedra
Golygons el sitio de Harry Smith
Oeis A006718
Esta entrada participa en la Edición 5.4: Martin Gardner del Carnaval de Matemáticas, cuyo anfitrión es Gaussianos.
Esta entrada ganó como mejor post de dicha edición del carnaval de matemáticas
Si lo quieres compartir o guardar



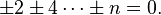
























el mínimo golígono con aristas primas es el siguiente:
ResponderEliminarAristas 8:
359S, 367E, 373N, 379W, 383N, 389W, 397S, 401E
ya que: -359+373+383-397 = 0 367-397-389+401 = 0
El dibujo te lo mando por email, pero ya comprobé que las aristas NO se cruzan entre si, como puede ocurrir con un golígono "defectuoso"
Corrijo: debe ser: ya que: -359+373+383-397 = 0 367-379-389+401 = 0
EliminarTe mando éste golígono porque el que está previamente publicado tiene una arista no prima: "1"
ResponderEliminar"Mínimo" aplicable sólo para una cantidad de aristas igual a 8. Falta encontrar el mínimo con 16 aristas. Puede ser que el mínimo de 16 aristas sea menor que el mínimo de 8 aristas, en el sentido de que la suma de todos los primos empleados sea una menor cantidad en la de 16 aristas que en la de 8 aristas cuya suma de todos los primos es 3,048.
ResponderEliminarAdemás, creo que con este polígono de 8 aristas también se puede teselar el plano infinito. ¿Alguien puede conformar o refutar esta creencia?
ResponderEliminarObtuve este polígono primo de 8 aristas con la ayuda de Excel y el Add-in ZZmath. Encontré otras 2 soluciones para 16 aristas, pero en ambos casos se "cruzan" las aristas, solución que geométricamente se considera inválida, creo.
ResponderEliminarAsí es Carlos, si se cruzan no es válido.
EliminarNo conocía estas figuras. Muy interesante.
ResponderEliminarVicente iq.
Golígono mínimo de 16 primos consecutivos desde 173 hasta 257, con una suma total de 3424: 173S, 179W, 181S, 191W, 193N, 197E, 199N, 211E, 223N, 227E, 229N, 233E, 239S, 241W, 251S, 257W.
ResponderEliminarYa que:
-173-181+193+199+223+229-239-251=0
-179-191+197+211+227+233-241-257=0
Figura mor Gmail
Gracias Claudio por publicar los croquis. Hago la aclaración de que en ambos casos (8 y 16 primos) los croquis son indicativos de la forma de los golígonos, pero no han sido hechos a escala exacta.
ResponderEliminarSi no he cometido error en mis dos búsquedas y efectivamente lo que te he mandado son los golígonos mínimos para 8 y 16 aristas primas, entonces el mínimo de estos dos es el de 8 aristas primas. Claro, todavía falta investigar en los casos restantes: 24, 32, 40 ... aristas. Así que el problema sigue vivo y es este: ¿Cuál es el golígono mínimo de primos consecutivos?... Creo que este será la materia del siguiente puzzle en mi sitio. Gracias por todo Claudio!
ResponderEliminar